男同打屁股对于“四色问题”的诠释

发布日期：2024-10-06 13:45 点击次数：100

男同打屁股对于“四色问题”的诠释

阐发：这是作家自投稿男同打屁股，本站莫得作念任何审核与蹧蹋，发表该文并不虞味该文正确。

“四色问题”是寰球数学史上一个特地知名的诠释艰苦，它条目诠释在平面舆图上唯有效四种口头就能使任何复杂阵势的各块相邻区域之间口头不会类似，也即是说相互之间齐有接壤的区域最多只可有四块。一百五十多年来有许无数学家用了很永劫期，化了许多元气心灵才智诠释这个问题。前些日子报刊上曾有报说念说：有好几位大学生用好几台电子野心思连合起来化了十几个小时才诠释了这个问题。本东说念主在二十多年前就知说念有这样一个“四色问题”，可一直找不到诠释它的才智。当前我刚斗争到“拓扑学”，其实用“拓扑学”旨趣一分析，“四色问题”就象当年欧拉把“七桥问题”当作是进程四个点不类似的七条线段的“一笔画”一样浮浅，连一般的小学生齐能诠释它。

证据“拓扑学”旨趣，任何复杂阵势的每一块区域齐可当作是一个点，两块区域之间相互有接壤的可当作这两点之间有连线，唯有诠释在一个平面内，相互之间齐有连线的点不会跨越四个，也就诠释了“四色问题”。

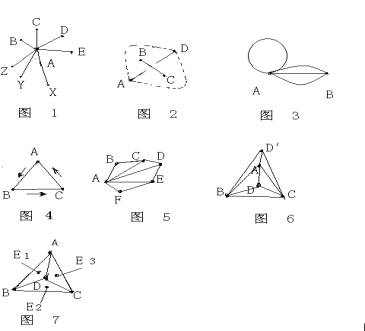
平面内的放肆一个点A可与许许多多的点B、C、D……X、Y、Z有连线（如图1所示），相同B点也可与其它点有连线，C、D……X、Y、Z各点也可与其它点有连线。但有一个原则：各连线之间不可相互交叉，因为一朝交叉就会产生一条连线陡立另一条连线（如图2所示），BC的连线就陡立了AD的连线。但有东说念主会说：两点间的连线可有许多条，AD连线可绕到B点或C点之外（图2中虚线所示）不就莫得交叉了吗？然而这样一绕就产生一个恶果：原本在一个闭塞图形外的点变成了闭塞图形内的点。底下就通过对闭塞图形的分析来诠释相互之间齐有连线的点不跨越四个。

一个点本人或两个点之间的连线齐可形成一个或多个闭塞图形（如图3所示）。三个相互之间齐有连线的点从A点连到B点再到C点又回到A点（如图4所示），必定会形成图形的闭塞。闭塞图形上的点若多于四点（如图5所示），从第三点C起各点与第小数A的连线又将悉数闭塞图形分割成许多小的闭塞图形。因此得出论断①：兼并平面上任何三个相互之间齐有连线的点，它们之间的连线必定会形成至少一个闭塞图形。咱们而况叫作三点连线闭塞定律。

平面上任何第四点不错是在上述三点连线组成的闭塞图形内，也不错在闭塞图形外（如图6中D点和D′点），D点可分离与A、B、C点有连线，D′点也可分离与A、B、C点有连线。D点与A、B、C点的连线把闭塞图形ABC分割成三个小的闭塞图形，D′点与A、B、C点的三条连线中一定有一条被夹在另两条中间，图6中D′A线被D′B线与

D′C线夹在中间，A点被闭塞图形BCD′所包围，与D点在闭塞图形ABC中情况交流。因此得出论断②：兼并平面上任何四个相互之间齐有连线的点中，必定有一个点被另三个点连线所形成的闭塞图形所包围。咱们而况叫作四点连线包围定律。

那么平面上有莫得第五点能分鹩肷鲜鏊牡愣加辛吣兀渴紫日獾谖宓鉋若要与第四点D有连线就必须也在闭塞图形ABC内部，其次这第五点不可落在各条连线上，不然会陡立这条连线。第五点只可落在E1、E2、E3位置（如图7所示），而这三个位置上的点分离只可与包围它的小闭塞图形上的三个点有连线，而不可与第四点有连线，若要有连线必定会陡立其它连线。因此得出论断③：兼并平面上任何相互之间齐有连线的点最多只可有四个，若第五点要与这四点有连线，必定会使其中两点的连线中断。咱们而况叫作五点连线必料定律。这即是条目诠释的“四色问题”。

以上是在兼并平面上诠释了“四色问题”。要是各区域图是分散在立体形的名义（比如地球仪），咱们证据拓扑学基首肯趣不错把这个立体形当作扁平形的，把图6中的D点当作在平眼前，把D'点当作在平面后，这两点若要有连线除非从平面中穿孔而过好像从立体形名义外的空间跨曩昔，不然这两点被闭塞图形ABC所离隔是不可能有连线的。这个立体形不错是唯有中间不穿孔的任何阵势，因为无论你名义怎样棱棱角角、凸凹叛逆，从拓扑学来看齐与球形是一样性质的，这好比一个气球在充气前不错是任何阵势，充气后老是接近球形。但立体形中间有穿孔的情况就不同了，它临了不会变成球形只可变成车轮内胎状的环形，前边的第四点与后头的第五点能通过中间的孔有连线。上头还提到的从立体形名义外的空间跨曩昔，跨曩昔的部分骨子上与原本的立体形组成了一个环形，临了也能变成车轮内胎状。是以得出论断：中间没穿孔的立体形名义上相互之间齐有连线的点最多只可有四个。